卷积神经网络是由多层感知机下演变出来的,多层感知机在训练时无法做到端到端(即从像素到分类结果),而是通过将图像处理成一维张量作为输入进行计算,这会忽略图像的邻近像素的空间特征,使得准确率不高。
CNN主要是由卷积层,池化(汇聚)层以及全连接层构成的。
卷积层:
卷积层是做了一种运算。将卷积核放在图像上进行移动,窗口移动到哪个位置,就对当前位置的像素值乘对应卷积核的数值最后累加得到这一次计算的结果,也是作为输出图像的其中一个像素。这就是和多层感知机不同的点,它考虑了周围像素,使得卷积后的像素获得一定的感受野,随着层数增多,每个像素感受野也会随之增多。卷积核移动完后得到的结果也就是特征图,也可以说是卷积的结果。
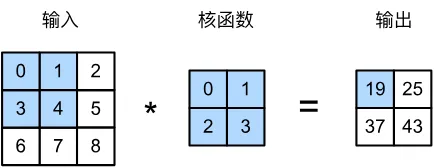
为了使图像长宽可以灵活变化,卷积操作除卷积核大小外还有两个参数,一个是填充Padding,另一个是步幅Stride,首先是填充,当Padding=x时,会在图像上下左右各添加x行或列;其次是步幅,当Stride=x时,卷积核每和图像进行一次卷积运算后,就会移动x再做下一次计算。填充和步幅的灵活搭配使得卷积操作可以保留当前长宽或者长宽变化,间接使得网络可以变得更深。对此,有以下计算公式计算图像经过卷积后像素的变化,
设原图像(通道为1)大小为(Nh,Nw),卷积核大小为(Kh,Kw),填充为(Ph,Pw),步幅为(Sh,Sw),则卷积后图像像素大小为

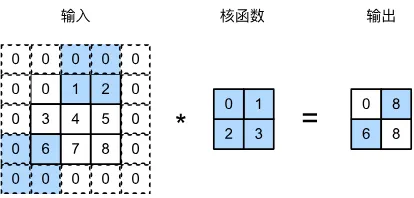
这里举个例子,原图像3×3,卷积核2×2,填充1,步幅为(3,2),代入公式后得到图像大小为2×2。
紧接着是多输入输出通道,多输入通道很好理解,日常生活的RGB彩色图像就是三通道,这也是目前图像训练常见样本的输入通道起始数。下图为两个输入通道的互相关计算。
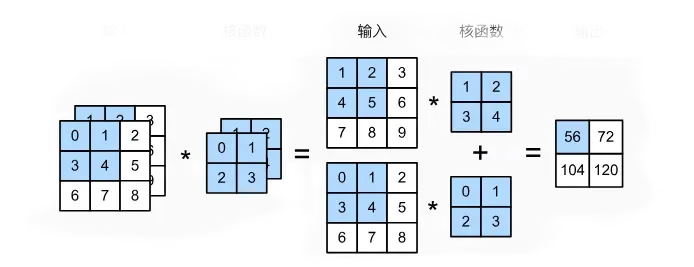
由上图可见,其输出通道为1。我们可以使其通道数变大,这样是为了学习更多的特征。这也是通过减少空间分辨率以获得更大的通道深度。所以,我们可以增加卷积核的维数,上图卷积核大小为CixNhxNw,再多加一个维度CoxCixNhxNw,这样一来输出通道数变为Co,达到多输出通道效果。
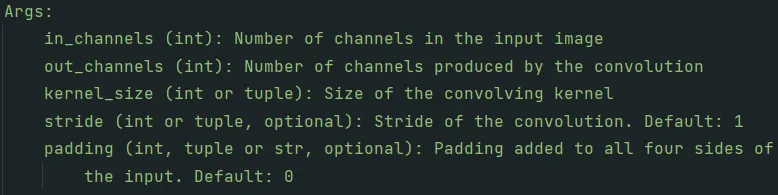
在python编程中,Pytorch提供内置函数nn.Conv2d,其中包含以下参数,刚上面所描述的如输入通道,输出通道,卷积核大小,步幅和填充都是常见参数。
池化层:
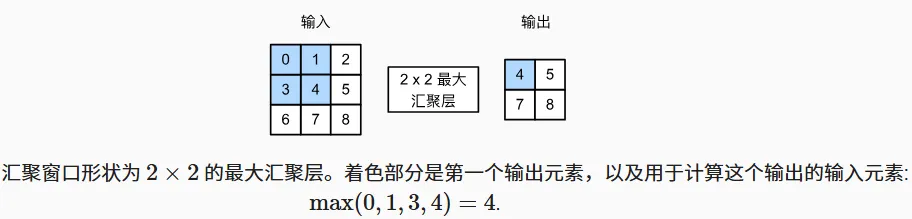
接下来是池化层,由于卷积层对位置信息比较敏感,随着卷积进行,每个神经元的感受野逐渐增大,使得网络能捕捉到更大的图像上下文信息,为缓解卷积层的敏感程度,池化层起到不错的效果。它的工作原理和卷积差不多,用一个窗口在输入上滑动并计算(常见的包括最大池化和平均池化)得到输出。下图为Maxpool计算。
同样地,池化层也拥有步幅和填充参数,这也使得池化层能够使图像感受野加大。不同于卷积,它没有多输入输出通道参数,这是由于池化层作用于多输入通道输入时,会一一对应每一个输入通道,它并不会融合通道,这也意味着输出通道数等于输入通道数了。所以说,池化层并没有需学习的参数。它不会使模型变大。
Pytorch内置函数为nn.Maxpool2d,参数包含下图所显示的。

全连接层:
最后是全连接层,就是之前在人工神经网络,多层感知机中常见的。下图为基本的单层神经网络。

每一个输出都是由四个输入分别乘对应权重最后求和得到。图像经过特征提取最后通过全连接层得到分类结果。选取值最大的标签作为本次分类结果,这为基本CNN的思路。但是全连接层弊端很大,基本上考虑就是其带来参数量过大,占用太多的显存。如今很少使用。nn.Linear()参数args包含输入特征数,输出特征数,偏差默认为True。
卷积层和全连接层反向梯度传播公式推导:


总的来说,卷积层其实是特殊的全连接层(向量->矩阵),CNN实现了端到端检测。以上参考花书。
